Il triangolo è una forma geometrica, cioè un poligono con tre lati e tre angoli e ha anche queste quattro caratteristiche:
- La somma degli angoli interni di un triangolo è 180°
- La somma degli angoli esterni di un triangolo è 360°
- In ogni triangolo uno dei lati è sempre minore della somma degli altri due.
- In ogni triangolo uno dei lati è sempre maggiore della differenza tra gli altri due.
Per poter comprendere al meglio le figure geometriche è necessario capire qualcosa in più in merito alla geometria di Euclide. È una disciplina molto antica e il suo nome deriva dalle parole greche “GEO” (terra) e “METRON” (misura) e originariamente raccoglieva tutte le tecniche necessarie per misurare un terreno.
I più grandi studiosi di geometria furono i greci e in particolare Euclide, grande matematico che scrisse intorno al 300 a.C. il libro “elementi”.

Ora vediamo quali sono gli elementi costitutivi del Triangolo:
LATI–ANGOLI–VERTICI.
Oltre a questi elementi il triangolo ne possiede altri chiamati elementi notevoli:
ALTEZZE–MEDIANE–BISETTRICI–ASSI
Inoltre, il triangolo può essere suddiviso e classificato in 3 tipologie di triangolo in relazione all’ampiezza dei suoi angoli:
- TRIANGOLO OTTUSANGOLO (UN ANGOLO INFERIORE A 90°)
- TRIANGOLO RETTANGOLO (UN ANGOLO = A 90°)
- TRIANGOLO ACUTANGOLO (TUTTI GLI ANGOLI MAGGIORI DI 90°)
A ciò aggiungiamo che il triangolo può essere suddiviso e classificato in altre 3 tipologie di triangolo in relazione alla misura dei suoi lati:
- EQUILATERO (TUTTI I LATI DI MISURA UGUALE)
- ISOSCELE (DUE LATI DI MISURA UGUALE)
- SCALENO (TUTTI I LATI DI MISURE DIVERSE)

Concludiamo ora con il comprendere come si calcola l’area del triangolo, cioè la superficie occupata da un triangolo e come si misura.
La formula più semplice consiste nel moltiplicare la misura della base per la misura dell’altezza, il risultato diviso per due.
Esiste una formula più complessa, ma altrettanto efficace e precisa, quella di Erone di Alessandria (matematico e ingegnere vissuto nel primo secolo d.C.)
Ora vediamo come calcolare l’area di questo triangolo con questo tipo di formula:
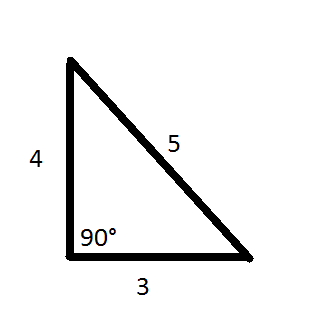
Prima dobbiamo ottenere il semiperimetro (metà del perimetro)
Dopodiché è necessario effettuare queste 3 operazioni: sottrarre dal semiperimetro ogni singolo lato del triangolo. Quindi:
6 – 5 = 1
6 – 4 = 2
6 – 3 = 3
Ora moltiplicare il semiperimetro per le tre differenze ottenute. Quindi:
6 x 3 x 2 x 1 = 36
Ora l’area del triangolo, secondo la formula di Erone, sarà la radice quadrata del risultato finale, cioè 36.
Pertanto, √36 = 6
